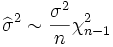Jason Rennie's Research Pensieve

9/14/06 - Screen process to test low-rank issue is on karhu.
9/14/06 - Low rank S issue: L^{^}L is PSD and Λ is PSD, hence, their sum is PSD. We can only get a low rank S if one of the entries of Λ is zero (or negative). Hmm... trouble is I'm getting low rank even when all entries of σ are non-zero!!! What's going on here?
9/14/06 - What I should really be doing in order to determine the stopping point for CG is to calculate CV error after every single/10th/100th iteration. The point at which error plateaus is where I want to draw the cutoff. I'm running into the problem that a single setting of eps may yield very different numbers of iterations in learning each of the class models, which may be a reason for thie somewhat high rates of error.
9/14/06 - What comes next after the factor analysis work? I need to do the text clustering experiments I've been planning to do for some time. See e-mail thread w/ Ron from June 7th. He used a number of different data sets for experiments in his ICML paper and has sent me pre-processed versions. I just need to run experiments. Compare vs. mixture of multinomials and mixture of mixture of multinomials.
9/14/06 - There actually isn't any need to randomize the data since we are selecting equal batches from each class. Only reason for the randomization would have been to ensure close to uniform distribution of items of each class. Randomization only makes comparison more difficult. I'm going to strip out the randomization code.
9/13/06 - CV code is ready-to-go. It's even set up to work in a distributed fashion. I just need to start it running. Only remaining thing that would be good to do would be to determine the best epsilon value. I think 1e-3 is a good value, though I might use 1e-4 to be safe. Would be good to do some test runs to see if there's any difference between 1e-3 and 1e-4 (in terms of error).
9/13/06 - I have cross-validation code working. One thing I realized is that I should randomize the order of the data before doing the cv splits.
9/13/06 - The normalization constant in faML.m isn't a problem. The only part I didn't include is only a function of the size of the data set (n and d). For the preliminary experiments I've done, n and d were fixed. I've modified faML.m to calculate this additional constant so that there are no issues with the cross-validation experiments.
9/13/06 - Something just occurred to me---do I need to normalize the model for evaluation? I.e. when I calculate negative-log likelihood on unseen data for testing, do such values need to be properly normalized? I would think so since the digit models have different parameters and hence different normalization constants. Fortunately, we don't have to worry about normalizing the trace norm, just the Gaussian from the factor analysis model. I.e. we need to modify faML.m so that it yields normalized NLL values.
9/12/06 - I published the write-up of Factor Analysis derivatives. I've also had success with test runs of conjugate gradients. I am able to achieve convergence for a variety of values of lambda ∈ {1,10,100,1000}. Next, I need to do some real experiments. My main interest is in comparing traditional factor analysis (FA) to FA w/ a trace norm prior in place of the rank constraint. To do this, I should use cross-validation on the training set to select the regularization parameter for each model (rank for FA, lambda for trace norm prior). I don't think it's worth doing much with the gamma parameters. Probably best just to set them to reasonable values and not worry about them! I've been using alpha=1,beta=10, but I think alpha=1,beta=1 is probably the most simple and straightforward choice. I think 5-fold CV is a good choice (esp. considering how long some of trace norm prior runs take), but I should make the code general enough to do 10-fold CV.
9/8/06 - Okay! Not only does the code seem to be working (using random initialization), but I've had additional successes---after enough iterations (e.g. 10k), error goes way down, to, and below, the best levels I've seen so far (not far from the 5% noted in the README file for the data). Things I need to do today: (1) finialize and publish my write-up of factor analysis math, (2) make a plan for running the experiments, start writing the code.
9/7/06 - Wrong! Low rank S actually yields -∞ objective; i.e. the probability measure changes when dealing w/ low rank S. Hmm... for now, let's try going back to random initialization. Need to think about this a bit more.
9/7/06 - Answer to the low rank problem: a low rank S yields an infinite NLL (since normalization constant in Gaussian likelihood will be zero due to det(S)).
9/6/06 - To make optimization faster, might be good to initialize U & V so that U*V' is equal to the maximum likelihood value for Lambda.
9/6/06 - Another advantage of FA w/ trace norm prior is that it can vary the rank according to the needs of the problem. I.e. for our digit multiclass classification problem, simpler digits (e.g. "1") may yield a lower rank than more complex/nonlinear digits (e.g. "8").
9/6/06 - Code checks out, even works for 10 iterations and bests regular trace norm code by a small amount. When I upped to 100 iterations, I ran into a rank error where rank(S) was less than 256. However, when I modified the error message to produce more information and re-ran the code, I didn't get the error. Not sure if this is a real problem that I need to spend some time thinking about...
9/6/06 - Hmm... length of vector is d*(k+2)+k*k. Solving for k is a quadratic problem. Wikipedia provides a good reference for solving quadratic equations. Since d > 0, we always get the positive solution. Just use the quadratic formula.
9/5/06 - Derivatives wrt U and V are written up. Just neet to touch up the writing a bit and publish. Then, need to implement the objective/gradient code.
8/24/06 - Next: write up derivatives of J₁ through J₄ wrt U and V. Matlab code for trace norm prior FA is faTN.m.
8/22/06 - Next: write up how to use trace norm prior.
8/22/06 - It works!!! Factor analysis code is up-and-running. Performance is even better than the linear classifiers.
8/22/06 - To do today: rewrite entire FA write-up w/ σ as parameter for covariance matrix diagonal.
8/22/06 - Another idea for factor analysis/trace norm: assume each data point generated from a separate Gaussian (identity covariance matrix), penalize rank of matrix of stacked mean vectors.
8/21/06 - ψ (the covariance vector for the noise data) must be constrained to be non-negative. This is easily achieved by reparameterizing so that ψ = σ². This is the first order of business tomorrow! Rewrite the ψ derivatives in terms of σ.
8/21/06 - To generate multivariate normal data, generate standard normal data, X₀ ∈ ℜ^{n
× k}, multiply by the transpose of a matrix Λ ∈ ℜ^{d × k}, then add μ ∈ ℜ^d to each row:
X = X₀*Λ^T + μ
As n → ∞, the mean of the data goes to μ and the covariance matrix goes to Λ*Λ^T.
8/18/06 - I recall that learning natural parameters of a Gaussian (mean and inverse covariance) is convex, but learning for other parameterizations (e.g. covariance matrix) is not convex. This means that any minimum we find may be local. However, this does not explain the behavior I'm seeing. The code isn't even finding a local minimum (gradient doesn't go to zero).
8/17/06 - Hmm... I tried learning a very simple example and even when I crank up the # of examples, the learned parameters don't match the original parameters...
8/17/06 - The Ghahramani/Hinton tech report on Mixtures of Factor Analyzers includes (beginning section 2) a nice reminder of how to convert a standard normal variable into any Normal. Wikipedia's Multivariate normal distribution page also has the reminder information: a n-dimensional random variable X is a multivariate normal if it can be written as X=AZ+μ where A ∈ ℜ^{n
× m}, Z is a m-dimensional standard normal, and μ ∈ ℜⁿ.
8/17/06 - What we need is a simple test-bed. A simple problem for which we know the answer. How about 100 samples from a zero-mean Normal with covariance matrix Lambda*Lambda'+diag(psi) where psi=[1 1] and Lambda=[1;1]?
8/17/06 - Hmm... gradient descent is producing negative entries in psi. I shouldn't be surprised. Negative entries in psi does not mean negative entries in S. And, since Lambda is rank-constrained, there may be cases where, in order to get the desired off-diagonal values, it is advantageous to offset the diagonal values of Lambda*Lambda' with negative values of diag(psi). We need to constrain the elements of psi to be non-negative. Also, note that the initial values for psi must be positive!!!
8/16/06 - Okay, I have the gradients for Factor Analysis (with prior on the inverse variance diagonal). Time to code them up and see if gradcheck2 gives them a passing grade! :)
8/14/06 - Would also be good to break apart the objective into smaller piecs and attack each piece separately---calculate partials wrt \mu, \psi, and \Lambda for each piece. I think this will make the whole calculation easier as I won't lose context between different variables. The way that each variable is handled for each piece is very similar. When I do all pieces of the objective for a single variable, I forget how I did the first chunk when I move onto the next variable.
8/14/06 - We've been sloppy about the \sum_j (from the prior). Need a different index from the variable that we're differentiating wrt. For \psi_j, we probably will simply be left with S_{jj}, but for L_{ij}, the interaction will be more complicated.
8/10/06 - Okay, it looks like I've calculated and implemented the derivatives for ML factor analysis. But, I haven't integrated the prior on psi. Need to do this today. Also wouldn't hurt to clean up the writing a bit.
8/8/06 - I calculated, implemented and tested the Factor Analysis derivatives for mu and psi. Just have L left to do.
8/8/06 - It appears that S. Geisser's "The predictive sample reuse method with applications" (1975) was the first paper to show that LOOCV is biased and to suggest something like k-fold cross validation in its place.
8/8/06 - It's known that LOOCV is biased. I wonder if that might have effected learning of hyper-parameter... Don't worry about this for now.
8/7/06 - In addition to the generative/Gaussian FA model extension, I should also apply the trace norm as regularization to the linear classifiers (logistic, smooth hinge, (modified) least squares).
7/27/06 - Would be nice to do the LOOCV hyper-parameter training using a bound on the classification loss. But, don't worry about this now... need to get working on factor analysis.
7/25/06 - Okay! I now have results for (diagonal covariance matrix) Gaussian likelihood, and multi-class classification using a variety of (linear) loss functions.
7/25/06 - The i=1 case of sandbox.m for ~/project/factorAnalysis is a good example of how much difficulty the code can have with a non-convex function. This could easily be made more efficient. For example, the code is re-calculating the same obj/grad.
7/25/06 - It works! Betas for all digit classes are found w/o problem. Has trouble with i=1 due to non-convexity. Would be nice if we could try backtracking or secant first based on whether we are in a concave or convex (respectively) region...
7/25/06 - I created a pround(x,p) function which rounds to the specified number of digits of precision. I used this for objective comparions in the line search and conjgrad and this fixed the issue I was seeing. Ultimately, we should be satisfied if either (1) the objective is decreased, or (2) the gradient magnitude is decreased and the objective does not increase.
7/25/06 - Need to modify the CG & line serach code to ignore differences beyond 10 significant digits (digits are noisy at about #14).
7/24/06 - diagonal.m is rewritten. I also added verbosity print-outs to diagonal.m and diagonalLOOCV.m to help display CG progress. One thing I noticed is that LOOCV learning of beta for digit 9 undesirably gets stuck in backtracking. Need to fix this.
7/21/06 - I need to rewrite diagonal.m so that it is parameterized in terms of mu and psi.
7/21/06 - Okay, I can now learn beta for all of the digit classes. What next? Well, I need to write a function that will calculate likelihood for each of the models (using Xi and b as the only inputs). Then, I evalute likelihoods on the test data!
7/21/06 - I fixed cgLineSearch.m. I correctly deduced the problem. Once I set alpha=1 and didn't break (so that it could calculate obj/grad w/ new alpha), it natural left the loop and went into backtracking mode, which found a reasonable step-size, 1e-4 (much better than the 1e-10 that it had been using!). It'd be nice to fix the "negative alpha" warning message to indicate that this is normal for a non-convex function.
7/20/06 - I think the solution is to set alpha to a large value (e.g. alpha=1), update obj & grad (via an ogfun call), then "break." If alpha=1 isn't a good choice, the backtrack code will be triggered, decreasing alpha until a semi-reasonable choice is found.
7/20/06 - Hmm... what appears to be happening is that the default step size of alpha=1e-10 is used if the non-linear approximation doesn't work (yields negative alpha). So, the change is in the correct direction, but it's so small that we never see any progress in the objective. What we should do is switch to backtracking (from a moderately large step size, such as alpha=1) if/when the non-linear search fails.
7/20/06 - I've realized one problem with the optimization of the hyper parameters---the (1-D) optimzation surface (for β) ain't convex. I've found an example where the surface is quasiconvex (level sets are convex), but not convex (i=8). Potentially, this might be wrecking havoc with the line search. I thought backtracking was supposed to handle this graciously, but apparently not!
7/17/06 - One thing is that it might be good to use the biased (ML) estimator of variance. It seems that we might have to do additional compensation due to the unbiased variance estimator...
7/17/06 - We need to make sure that the average of the ratios (eqn. 17) is unity (or log of left-side is null). What's a bit tricky is that the top of the ratio is the squared difference for example i, and the bottom of the ratio is the average squared difference of all examples except example i.
7/17/06 - What might work well is to set α=1 and find the β that minimizes the LOOCV likelihood. My simple 1-D example suggests that this approach might work---for any value of α it appears that there is a value of β which minimizes the likelihood. The reverse clearly doesn't hold---there are values of β which are too small and would not allow us to minimize the likelihood. The real question: can we prove that given fixed α, we can always find a likelihood-maximizing β?
7/17/06 - There seems to be a chicken-and-egg problem here. We'd like to set β or α to a constant and solve for only the other variable, but what if we choose poorly and we can't achieve the minimum with that setting?
7/17/06 - I've plotted the LOOCV log-likelihood as a function of α and β. Though not immediately obvious, it appears that there is no single solution, but rather a trough of solutions along a line in the α/β space. Note that α and β only effect the objective via the LOO inverse variance, ψ. Though there are two parameters, ψ bottlenecks their effect. In fact, using the formula for ψ, we can determine the line(s) in α/β space in which ψ (and hence the objective) is constant. Let D be the summed differences. Let ψ be fixed. Solving for α & β, we get
n-2-Dψ = βψ-α
The left side of the equation is constant, so it defines a line along which ψ remains constant.
7/13/06 - Need to do constant manipulation so that we can interpret α as effective sample size and β/α as the empirical variance of the simulated examples.
7/12/06 - Okay, so I've figured this variance prior thing out (use Wishart/gamma as a prior on the inverse covariance matrix). I've even worked out the math for a single training example. Need to extend the math to a full set of training data.
7/12/06 - Page 5 of The Matrix Cookbook gives the relation between the determinant of an inverse and the determinant of the original matrix: det(A^-1) = 1/det(A).
7/12/06 - This paper by Geiger/Heckerman on the Normal-Wishart distribuiton says that the Wishart is the prior on the inverse covariance matrix (what they call the "precision matrix").
7/12/06 - Yes, Wishart is distribution of sum of outer products.
S = ∑_i=1ⁿ X_i X_i^T,
where X_i is a column vector, is distributed as a Wishart(V,n) if the X_i ∼ N(0,V) iid. So, to use Wishart as a prior on variance, it seems that we should multiply variance by n...
7/12/06 - Still some issues to deal with. The Wishart/chi-square/gamma is the prior for the sum of empirical covariances, right? I.e. we need to multiply variance by the number of samples before plugging it into Wishart/chi-square/gamma.
7/12/06 - Finally realized why a product of gamma's and the Wishart have different normalization constants when I use a diagonal matrix with the Wishart. The Wishart is normalized over positive definite matrices. Slapping on a diagonal matrix doesn't mean that it's normalized properly. To use the Wishart with our diagonal covariance matrix, we'd need to re-normalize. Of course, we'd just find that it's the same as a product of gamma's.
7/11/06 - The partition function of the Wishart distribution appears to be related to the volume of the stiefel manifold. Edelman's handout #4 (page 8) provides a relation between the Gaussian normalization constant and the surface area of the sphere.
7/11/06 - Wishart is the generalization of the chi-square distribution, which are both priors for the Gaussian variance. The gamma distribution is a prior for the inverse variance. What I wonder: if I set the positive definite matrix parameter of the Wishart to the identity, V=I, why isn't the Wishart pdf simply a product of chi-square pdf's?
7/11/06 - Wikipedia has nice discussions of maximum likelihood, maximum a posteriori, and (a very brief discussion of) regularization.
7/9/06 - Chat w/ Tommi about variance priors. While the chi-square (gamma) is the distribution of sample variances, the gamma is (also) the conjugate prior to the variance (for a 1-d Gaussian). Generally, the Wishart distribution is the conjugate prior to the (inverse covariance matrix of the) Gaussian. The Normal is conjugate prior for the mean. Hence, the Normal-Wishart distribution is the full conjugate prior to the Normal distribution. Tommi says that when the Gamma is taken as the prior to the inverse variance (diagonal covariance) and the variance is integrated-out, we get Student's t-distribution. Hmm... I thought I might want to use the t-distribution, but now I think not. The t-distribution would be approprite if I had a Gaussian w/ diagonal covariance and I wanted to impose a prior and eliminate variance as a variable (to be replaced by parameters of the t-distribution). But, I don't have this situation. My Gaussian distribution has a complex covariance matrix with two separate priors. One trace norm prior and one (I have now decided) Gamma prior. I don't think there's anyway I could marginalize over the variance variables.
7/8/06 - Hmm... I'm seeing cracks in my idea. There's a good reason for the specified number of degrees-of-freedom. Chi-square yields a distribution of sum-of-squared values. I.e. to get (sample) variance, you need to divide by the number of samples (size of the sum). Now, if the parameter corresponding to the number of samples is allowed to be ℜ, it's less clear what to do. Do we divide by 2α+1? I.e. the prior is g(x/σ²/(2α+1)|α,1/2)?
7/8/06 - We're not quite done yet. g(x|α,1/2) isn't the prior. g(x|α,1/2) is the prior on values scaled by 1/σ². I.e. g(x/σ²|α,1/2) is the prior.
7/8/06 - Yes, I think we can. As Wikipedia notes, the chi-square distribution is a special case of the gamma distribution. In particular, if f(x|k) is the pdf for χ²_k and g(x|α,β) is the pdf for the gamma distribution, then f(x|k) = g(x|k/2,1/2). We get a prior with width-control by using g(x|α,1/2) as the variance prior.
7/8/06 - A problem with my idea is we have no control over the "width" of the prior. The width is controlled by the degrees-of-freedom, which are set by the number of data points. However, this is likely to be a poor choice. Better would be to select, k, the degrees-of-freedom, via cross-validation, or some-such. The fact that k is discrete is cumbersome. The chi-square is a special-case of the gamma distribution. Can we devise a nice prior which is a gamma distribution?
7/8/06 - Here's one idea: First, center the data (subtract mean from each column of X). Then, calculate the sample variance on the entire data set treated as a single vector (single-dimension random variable). Call this quantity σ². Then, use σ²χ²_n-1/n as the prior on the variance of each dimension of the data.
7/8/06 - One thing that Cochran's Theorem states is that the sample variance of n independent standard normally distributed random variables is a chi-square distribution with n degrees of freedom. It further states that the sample variance, ∑_i U_i², can be written as the sum of k < n variables {Q₁, …, Q_k} with ranks {r₁, …, r_k} such that Q_i ∼ χ_{r_i}². Also evident from Cochran's Theorem is the fact that the sample variance (computed using the sample mean), ∑ (X_i - X)² has n-1 degrees of freedom (multiply through by σ² in the Wikipedia example). In particular,

$\widehat{\sigma}^2\sim \frac{\sigma^2}{n}\chi^2_{n-1}$
7/8/06 - Wikipedia also has an entry for the Student's t-distribution, the basis for the t-test.
7/8/06 - The Chi-square distribution is the sample variance distribution. Cochran's Theorem provides the connection between the chi-square distribution and the sample variance distribution. Note that Chi-square is a special case of the gamma distribution. Also note that a variable Z is distributed according to chi-squared (with k degress of freedom), Z ∼ χ_k², iff
Z = ∑_i=1^k (X_i - μ_i)²/σ_i²,
where μ_i and σ_i² are (respectively) the mean and variance of X_i. I.e. Z = ∑_i=1^k Y_i is only distributed as chi-squared if the Y_i are each distributed as a standard normal.
7/8/06 - Note that we're modeling a covariance, which is really a sum of squares, i.e. S_ii = ∑_i x_i². We get a non-zero covariance by requiring that the data not be constant (a continuous distribution over data values would be sufficient). Hmm... if we put a Gaussian distribution over data points, what is the covariance distribution?
7/8/06 - One option would be to use the parameterization S_ii = exp(ψ_i)φ (or S_ii = exp(ψ_i + φ)) and apply a Laplacian prior to ψ_i. Note that the Trace Norm prior is a generalization of the Laplacian prior...
7/8/06 - In the Hinton/Dayan/Revow work, they simply added a small value to each of the diagonal elements to prevent zero variance (pg. 15-16)...
7/8/06 - Q: what do we really want to achieve with the prior? Let's assume no prior on φ. Using the S ≡ diag(ψ + φ) parameterization, no prior will prevent S_ii=0 if the data on dimension i is constant. Can we prove this? Consider a simple case: one-dimensional data, φ > 0 fixed. Assume that the prior on ψ is finite for ψ=-φ, i.e. P_ψ(-φ) < ∞. Note that if x_i=0 ∀i, then the likelihood is
P(x|ψ,φ) = (2π)^-n/2 (ψ+φ)^-n/2.
Note that as ψ → -φ, P(x|ψ,φ) → ∞. Hence, the prior on ψ must be infinite at -φ in order to prevent values of the covariance matrix from being non-positive.
7/8/06 - For the factor loading matrix, we are using a sum of singular value prior. That equates to sum-of-magnitudes for diag(S).
7/8/06 - How to regularize the diagonal covariance matrix? My first idea was set S ≡ diag(ψ + φ) where ψ ∈ ℜ^d and φ ∈ ℜ, and to apply an exponential(λ) prior to each value, P(φ,ψ) = exp(-λ∑_iψ_i - λφ). While the exponential prior is appropriate for φ, it is not appropriate for ψ_i, as ψ_i may take on any value ∈ [-φ,∞]. To use the exponential prior, we could re-define the covariance matrix, S ≡ diag(φψ). Then, φ is the base covariance and ψ_i is the multiplier for the i^th dimension.
7/8/06 - Code for psi works with artificial data. Doesn't work for real data, most likely b/c of zero variance for some dimensions. Need to implement regularization on psi.
7/8/06 - Okay, looks like I have a working version for psi. Just need to confirm that the learned values really are variances. Next, lambda. Also, I need to add regularization for psi to ensure no zero values. One option. Add new scalar parameter which is added to entire diagonal. Then, regularize psi with quadratic penalty.
7/7/06 - I have a draft gradient/objective function for factor analysis. It passes gradcheck2, but my conjugate gradients code does weird things: infinite objective values, negative step sizes (alpha), and too many resets. Something is wrong. I need to do a step-by-step re-derivation of the gradient. First, just do the gradient for psi, avoiding usage of formulas at the Matrix Reference Manual when possible. Then, checkgrad2 that and run some test data through (make sure that data has non-zero variance for all dimensions). Then, move on to the gradient for Lambda.
6/30/06 - Here's a useful tidbit: det(A^-1) = 1/det(A).
6/30/06 - First, I should try implementing PCA & Factor Analysis! That will give me somewhere to start for the trace norm extension. Might also be good to try a trace norm extension where we regularize the inverse covariance matrix. Isn't the determinant just the product of singular values (or something like that)? Couldn't we just take 1/det to get determinant of inverse?
6/29/06 - Okay, I think I have a decent FA write-up. Next, the text model...
6/27/06 - Went back and re-read my writings on the "bits-back" argument: Stochastic encoding and the ``bits-back'' argument and Encoding Model Parameters. Certainly would be nice to wrap my head around this further. But, I think it's going to be a bottleneck if I delve to deeply. In particular, encoding of parameters requires that we have two distributions for the parameters: one prior and one generating. The net encoding length is then the KL-divergence between these two distributions. I.e. we can't just multiply in the prior as one would normally do for maximum a posteriori. So, this will require a somewhat careful treatment. I'd like to discuss the Hinton et al. argumentation for why FA can be seen as an extension of PCA, and I'd like to use that as a basis for the addition of the trace norm prior.
6/27/06 - The coding framework used by Hinton/Dayan/Revow ties back to the Hinton/Zemel MDL/bits-back paper, which I have written about. In this framework, parameters are transmitted stochastically (additional motivation for Bayesian statistics/integrating out parameters). The coding length for parameters is the KL-Divergence between the transmission distribution and the parameter prior distribution.
6/27/06 - Re-reading the Collins/Dasgupta/Schapire Generalized PCA paper so that I can related trace norm clustering to clustering w/ Generalized PCA. Included in the paper is a nice discussion of exponential models. One observation I've heard many times that is worth committing to memory is the fact that given the log-likelihood of an exponential model:
log P(x|θ) = log P₀(x) + xθ - G(θ),
where θ is the "natural parameter," the derivative of G(θ) is g(θ) = E[x|θ]. Note that G(θ) = log ∑_{x
∈ X} P₀(x) e^xθ.
6/24/06 - Just sent Tommi an e-mail describing what I think I should do: write up my extension to FA w/ the trace norm prior as a continuation/extension of the Hinton/Dayan/Revow work without worrying about the fact that the new posterior isn't concave (FA likelihood/posterior isn't concave either, so I don't think I'm making things worse wrt concavity). Probably best to revise my currently-published FA writing than to start anew (it has some mistakes I need to correct anyway).
6/23/06 - Modification of FA will only have (a chance of) concave likelihood if we do the parameterization in terms of the inverse covariance matrix. It's as if we want the inverse covariance matrix to be the sum of the inverse factor loading matrix plus inverse noise matrix. 'course, it's not that simple... Maybe I should just throw in the towel... update my FA write-up describing how one could extend FA to incorporate a prior on the factor loading matrix and discuss how this provides a more complete model. But, it's not the "holy grail" that one might hope for as the resulting model still has a non-concave posterior. And, optimization may be complicated as I think the gradient will require a matrix inverse (though on a task like 8x8 digit recognition, this shouldn't be an issue).
6/22/06 - Tommi says: Gaussian likelihood as a function of inverse covariance is concave. This is a bit troublesome since it's not the inverse covariance that we're regularizing, but rather the factor loading matrix, which is added to a diagonal matrix to yield the covariance matrix. So, the posterior (including the trace norm prior) would almost certainly not be concave. Maybe this isn't worth worrying about... though convexity is certainly a significant argument for why trace norm should be used...
6/21/06 - Notes from the Hinton/Dayan/Revow paper:
- Idea is to use mixture of generative(-ish) models to classify images of digits.
- Their view is that PCA is the simplest model: it only models the cost of transmitting errors---it ignores the costs of communicating the principal components (PC), and of communicating the projections of each data point onto the PC (only the projection orthogonal to the manifold of PCs is counted in the error).
- Their view of Factor Analysis (FA) is as the next step---FA accounts for the cost of encoding the data points onto the factors/components. But, it still doesn't account for the encoding of the factors/components.
- Another difference between the algorithms is that PCA effectively assumes equal variance of the different dimension, whereas FA has parameters to allow for different variances.
- Our extension of FA takes care of the remaining encoding---the trace norm prior accounts for encoding of the factors/components. The regularization constant (λ) remains, but this is insignificant for most applications
- In their FA experiments, they provide some regularization of the noise parameters (Ψ/ψ). They observe that a single pixel may be constant in the training data, producing a covariance parameter of unity. The model will then give zero probability to any image which does not have the value of the pixel observed in the training data. To fix this, they add an additional global noise parameter, which is added to (all components of) ψ. By placing some prior on ψ, they avoid this undesirable case. Interesting that the simple hierarchical parameter model easily handles this issue (i.e. if FA were a model which fully encoded the data and model, it would not have been necessary to make this "fix").
6/20/06 - Okay, I've written up my extension of Factor Analysis. What now? Well, it might be good to read the Hinton/Dayan/Revow digit image classification paper to see how FA is used in a practice and how it compares vs. PCA.
6/16/06 - FA assumes that the underlying data is distributed as a zero-mean Gaussian with rank-limited covariance matrix Λ^TΛ. Additive noise is assumed to take the form of a zero-mean Gaussian with diagonal covariance matrix. To elimiate the hard constraint on rank, but encourage a low-rank covariance matrix, we could extend Λ to full size (n × p) and impose a trace norm distribution on Λ.
6/16/06 - FA is imposes a rank constraint on the "true"/noise-free data. In contrast, our trace norm version places a smooth penalty on the sum of singular values of the "true" data, effectively encouraging low-rank. This is closely relted to "matrix factorization" applications, which have seen substantial improvements in inference by moving from a hard rank-constraint to a soft, convex trace norm penalty.
6/16/06 - Factor Analysis is simply a Gaussian model with a constraint on the covariance matrix. Similar to what has been done with matrix factorization, we can remove the hard constraint and replace it with a soft, convex, penalty in the form of the trace norm. Optimization appears a bit tricky due to the Gaussian distribution (log-determinant and matrix inverse in the NLL).
6/14/06 - There's an interesting connection between factor analysis and modeling using the trace norm distribution as a prior. Maryam Fazel's thesis discusses two rank heuristics: the trace norm and the log-determinant. Factor analysis uses a multivariate Normal data likelihood, which includes a log-determinant term. The determinant is of the covariance matrix, so it might be intepretable as a parameter prior (though, it appears as part of the normalization constant for the Gaussian).
6/13/06 - The Mixture of Factor Analyzers (MFAs) model is a mixture of factor analysis models (duh!). Each FA model is allowed to have a different mean (the mean was subtracted from the data in the simple FA model). A new parameter vector is introduced to select between the FA models. As Ghahramani and Hinton note, "The mixture of factor analyzers is, in essence, a reduced dimensionality mixture of Gaussians."
6/13/06 - Factor analysis (FA) is a generative model where each data variable is the sum of linearly transformed factors (each of which is unit Normal) and Gaussian noise (zero mean/diagonal covariance). The dimensionality of the factors must be specified. The parameters to be learned are the "factor loading matrix" (linear transform from factor-space to data-space) and the (diagonal) noise covariance matrix.
6/13/06 - Sounds like the Mixture of Factor Analyzer idea is very similar to what John and I are doing with trace norm clustering. The "mixture" part corresponds to clustering; the "factor analysis" part corresponds to dimensionality reduction within each cluster.
6/12/06 - Collins/Dasgupta/Shapire paper: PCA finds linear projection of data points to low-dimensional space which minimizes sum of squared distances. This is equivalent to assuming that given data points are original data points perturbed with Gaussian noise (identity covariance matrix). Their generalization uses this view. They note that in the generalization, though the low-D parameters will lie in a linear sub-space, it may not be the same space as the data; hence, the parameter space may be non-linear in the data space. Good brief introduction to exponential family models. Useful note: derivative of partition function is expectation.
Notes: derivative of partition function is expectation; Δ is used to denote the simplex;
6/12/06 - There's a Ghahramani/Hinton tech report on Mixtures of Factor Analyzers.
6/12/06 - I figure the Collins/Dasgupta/Shapire Generalized PCA paper is as good a place to start as any (for gen. PCA). Might also be worth re-reading Elkan's DCM paper. There's also a new spectral clustering paper by Azran & Ghahramani at ICML '06 that might be worth reading.
6/12/06 - k-means is effectively the same as mixture of gaussians; other mixtures define a different loss function; natural parameter mixture uses a linear loss.
6/12/06 - In order to understand how TNC behaves, it's important to understand how other clustering algorithms behave. What are some standard examples? (1) k-means, (2) mixture, (3) generalized PCA, (4) mixtures of factor analyzers, (5) spectral. #3 and #4 are taken from UAI review #1.
6/11/06 - TNC: Need to compile library of small examples to exhibit how TNC works. E.g. points at corners of tetrahedron. Highlight properties: sensitive to outliers (less sensitive to number of points than least squares).
6/8/06 - Maxima doesn't know what to do with this integral:
∫₀^c x^a e^-bx dx.
or this one:
∫₀^∞ x^a₁ e^-b₁x dx ∫₀^x (x²-y²) y^a₁ e^-b₁y dy.
6/6/06 - The (revised) integral calculations for EP involve forms that are like (but not identical to) incomplete gamma functions. One of the simplest integrals we have to solve is
∫₀^c x^a e^-bx dx.
The problem is that in the incomplete gamma function, b=1.
6/5/06 - Alan and I resolved the issue w/ EP. Integrals we're doing must be over positive domain. I.e. we forgot the fact that the singular values are ordered σ₁ > ... > σ_m. The moment itegrals must be done with the constraint σ_i > σ_j. I.e. these integrals are (proportional to) incomplete gamma functions. Matlab implements this as gammainc.
6/5/06 - Bekkerman et al. paper:
- Based on Information Bottleneck. Basic idea is to simultaneously cluster documents and words, whereas earlier IB clustering work has only clustered documents.
6/5/06 - Rest of Today: read Bekkerman et al. paper and write-up notes.
6/5/06 - Draft implementation of expectation propagation. Significant issues with algorithm. Need to talk to Alan. Trace norm experiments: found a good paper to use as a basis for comparison: the Bekkerman/El-Yaniv/McCallum paper on Distributional Clustering. Experiments on 20 News and Enron e-mail. There's even a URL for Enron "prepared" data.
6/2/06 - Chatted w/ John about what needs to be done to get our paper in shape for NIPS:
1. Text and Biology experiments
2. Comparison to other clustering algorithms (esp. mixtures of factor analyzers and generalized PCA)
3. Small-scale experiments that provide intuition for how TNC works
4. Discuss consistency of normalization constant estimates
5/31/06 - From prior meeting w/ Tommi: need to do simple experiments w/ trace norm clustering to provide intuition. Give intuition for why it should work, how parameter affects the solutions.
5/30/06 - Ignore normalization constants. We start w/ all α_i, β_i set to unity. We calculate the leave-one-out parameters (eq. 7), we calculate integrals using the LOO parameters (eq. 8-13) (NOTE: this is simple calculation of moments of Gamma distribution), we update the α_i, β_i (eq. 16), and, finally, we update the ˜f_i,j paramters (eq. 19-21). Loop until convergence. Eq. 22 gives methodology for norm. const. calculation.
5/30/06 - Maybe the bookkeeping isn't too bad. q(σ) is a product of the ˜f_i,j(σ_i) and ˜f_i,j(σ_j) terms ∀ i,j. I.e. we must keep track of {η_i,j}, {ε_i,j}, and {s_i,j}. These parameters are all initialized to unity. For i fixed, q(σ_i) is a product of only the ˜f_i,j(σ_i) functions.
5/30/06 - So, how do we keep track of all the constants? Seems like it will require a lot of bookkeeping.
5/30/06 - Let f₁(x|α₁,β₁) and f₂(x|α₂,β₂) be two Gamma pdf's. The product of these two pdf's is:
f₁(x|α₁,β₁) f₂(x|α₂,β₂) = x^{α₁+α₂-2} β₁^α₁ β₂^α₂ e^{(β₁+β₂)x}/Γ(α₁)/Γ(α₂).
This is not a Gamma pdf. But, it has the correct form and merely needs to be properly normalized. I.e.
Gamma(x|α₁+α₂-1,β₁+β₂) = f₁(x|α₁,β₁) f₂(x|α₂,β₂) (β₁+β₂)^{α₁+α₂-1} Γ(α₁) Γ(α₂)/Γ(α₁+α₂-1)/β₁^α₁/β₂^α₂.
5/30/06 - Seems like a link to Wikipedia's Gamma Distribution article is in order.
5/30/06 - What Alan means by eq. 3 (product of Gamma pdf's) is that the ˜f_i,j functions are conjugate to the Gamma pdf. So, when you take the product of all of them, you are left with a product of Gamma pdf's (plus a constant term corresponding to the fact that the f's may not be normalized). So, the integrations in eq. 8, 10, 12 are over Gamma distributions.
5/24/06 - Had a chat w/ Alan. Shouldn't be too hard to implement the EP approximation of the trace norm dist. norm. const. The approximation distribution is initialized to the gamma part of the dist. A pair of approximation functions is used to deal with the difference of square terms---these are each initialized to unity. The full q is a Gamma. The leave-one-out step yields another Gamma w/ different shape & scale parameters. We compute moments of this leave-one-out Gamma, then update q by updating f_i,j which is updated by new settings of η_i,j, ε_i,j and s_i.
5/24/06 - Draft of chapters 2 & 3 complete, sent to Tommi for comments.
5/15/06 - Thesis update: 33 "draft" pages, 44 pages total.
5/11/06 - Thesis update: 32 "draft" pages, 43 pages total.
5/11/06 - Need to edit the Model 3 and antecedent model sections, make them consistent with the CRR problem section.
5/11/06 - Is there really a need for the max-antecedent model? The regular antecedent model doesn't (as far as I can tell) have a majority bias. This is because the antecedent decision is made independently for each mention. The flaw in my prior thinking was that we had to deal directly with cluster labels. In fact, this is only the case for learning if the training data does not include antecedent information. We never need deal with cluster labels for inference. We can simply determine antecedents and assign clusters according to antecedent connectivity.
5/11/06 - Thesis update: 31 "draft" pages, 45 pages total.
5/11/06 - Thesis update: 30 "draft" pages, 46 pages total.
5/10/06 - We need to write out the details of learning & inference for the antecedent model.
5/9/06 - For the hybrid model, we would like the antecent model to use feature values that capture not only the prospective antecedent, but also the mentions with which it is co-referrent. For example, if the prospective antecedent is ambiguous about gender or number, then the co-referrent mentions should be used to determine the gender or number.
5/8/06 - Model 3 and my antecedent model are very similar. In fact, if you strip constraints from both models, they are identical:
P(y|x) ∝ ∏_i,j exp[w^Tf(x_i,x_i,y_ij)].
The key is in the constraints. Model 3 allows only complete edge graphs, i.e.
y_ij + y_jk + y_ik ≠ 2.
In contrast, my antecedent model allows at most one outgoing edge per node/mention (assuming all edges point toward the earlier mention---mention with lower index),
∑_{i < j} y_ij ≤ 1.
There's no special form for Model 3, but there is for our antecedent model. For mention x_j, there are j possibilities: either there is no antecedent or one of x₁,...x_j-1 is the chosen antecedent. The probability of having x_i as the antecedent is proportional to the i-j potential. Note that the joint distribution is a product over pairs. I.e. it's a product of distributions over edges. Each edge has it's own normalization. To calculate the probability that there is no antecedent, we take one minus...
5/1/06 - Today: read over intro & 1st section of chapter 3. Do light editing as necessary. Then, start working on section 2. Print out Alan's EP write-up and read on the way home.
4/28/06 - Chatted with Alan about an EP approximation for the trace norm normalization constant. Basic idea is to approximate the whole thing as a product of gamma distributions. Seems like way too simple of an approximation to be useful, but there is the possibility of doing a tree approximation, where the approximation is a product of terms with one term for each pair of σ's. This has more promise in my mind, but it also sounds more difficult. Anyway, idea of the simple EP approximation is to integrate polynomial terms one-at-a-time, updating the mean and variance of each of the gamma distribution terms.
4/25/06 - Dumped lots of writing into the co-refernce chapter. 41 pages! Woo hoo!
4/25/06 - Working on the co-reference resolution chapter. One thing that would be really helpful is a list of the relevant write-ups. Here they are:
- Learning how to cluster with application to coreference resolution
  - Original formulation
  - Each non-terminal noun phrase points to exactly one other NP (directed graph)
  - (Broken!) reinforcement learning interpretation
  - (Weak!) mechanism design interpretation
  - Transition probability formulation. Transition probability associated with each directed edge; self-transitions represent terminal NPs (NPs that don't refer to another NP). Given transition probability matrix, we can solve via matrix inversion for the matrix of terminal probabilities (probability that each node will terminate at a given node).
  - Given training data, use maximization of the sum of the terminal probabilities as the objective. Constrain the transition probabilities to be log-linear functions of feature vectors. Since training data doesn't identify "roots," these must be learned as well (additional parameters).
  - Co-reference in a document is almost exclusively from bottom to top. This solves the root-identification issue. Also, matrix inversion no longer necessary---use dynamic programming. Can show "consistency." Instead of sum of probabilities, could use product, which is closer to traditional loss functions.
- The Equivalence of the Model of McCallum and Wellner (2003) to Minimum Cut and Maximum Inter-Cluster Similarity
- An Extraordinarily Brief Description of a Hybrid Model for Co-reference Resolution
  - First description of hybrid model (use (undirected) McCallum/Wellner for proper NPs, directed model for non-proper NPs). For each NP, assume all previous cluster labels are known. Goal is to maximize sum of transition probability that links to NPs with the same label.
- Learning Parameters for an Antecedent-based Co-reference Resolution Model
  - Longer version of "Extraordinarily Brief..."
- Inferring a Noun Phrase Clustering for an Antecedent-based Co-reference Resolution Model
  - The sum-objective (which is assumed) prefers to agglomerate nodes into one big cluster, especially when the transition probabilities are spread out.
  - A greedy algorithm can easily pick the wrong clustering. Figure 1. Greedy algorithm puts nodes 1 and 2 in different cluster. But, because node 3 is equally spilt between nodes 1 and 2, it's better that 1 and 2 are in the same cluster.
  - Suggestion is to try multiple greedy approaches.
- A Max-Antecedent Model for Co-reference Resolution
  - Flaw in sum-based model: majority bias.
  - Propose max-based model: NP is assigned to same cluster as prior NP with highest similarity/transition probability.
  - Clear definition of mathematics of model (equation 1).
  - Last two paragraphs are mediocre.
- Learning Parameters for a Max-Antecedent Co-reference Resolution Model
  - 1st para: a more careful write-up of the mathematics, including definition of similarity as a linear function.
  - 2nd+ para: note that as w changes, max-antecedent may change, which is the reason it is only locally convex; good description of an algorithm to find optimal weights
- Max-Antecedent is Convex Plus Concave
  - Title says it all: good note to include in discussion of objective.
- A Hybrid Model for Co-reference Resolution
  - sec 1: pretty good introduction to this work
  - sec 2: good description of the sum-model (not max-model)
  - sec 3: brief discussion of learning issues
  - sec 4: argument that using sum in hybrid model is reasonable b/c we separate learning of proper and non-proper NPs; no majority bias in non-proper learning because clusters are already fixed (by proper model). Majority bias still exists, but it won't affect number of clusters.
- Optimization of a Locally Convex Objective on Convex Regions
  - Lots of gritty details on how one might implement the max-antecedent optimization.
- A Class of Convex Functions
  - I don't think this is realted... might be related to log-log stuff.
- A Max-Margin Best-Previous-Match Coreference Resolution Algorithm
  - Good baseline to use for comparison (if I ever do experiments!)
4/24/06 - Started a thesis document yesterday. Dumped in the SIGIR paper, did some editing, dumped in a couple of relevant write-ups as appendices. Already up to 31 pages (!)
4/24/06 - Tom's Hardware has a recent review of 19" LCD Monitors. The Viewsonic VX922 takes the prize for quickest response times. The Viewsonic VP930 seemed to be the best overall monitor.
4/18/06 - John seems to have figured out the solution to minimization of GTN over y. It's very close to my supposed solution, √(1-x) + √(1+x), but it's not identical. The solution is
y = sin(tan^-1(-2*√[1-x²])/2)
Here's matlab code to plot the trace norm:
```
hold off;
x = 0:0.01:1;
y = sin(atan(-2*sqrt(1-x.^2))./2);
plot(x,sqrt(1-x.^2+2.*x.^2.*y.^2+2.*x.*y.*sqrt(1-x.^2).*sqrt(1-y.^2))+sqrt(1+x.^2-2.*x.^2.*y.^2-2.*x.*y.*sqrt(1-x.^2).*sqrt(1-y.^2)));
hold on;
plot(x,sqrt(1-x)+sqrt(1+x),'r');
  
```
When this is compared to the numerical computation (below), the numerical computation comes out below and lines up well with √(1-x) + √(1+x). So, this solution must be a local minimum...
4/18/06 - To avoid an additional symmetry, might want to do an r,θ version, x=r&sin;θ, y=r&cos;θ and restrict r ≤ 1. Note that since trace norm is invariant to rotations, it's invariant to row exchanges, so the case that second row is larger than first is described by some parameterization where first is larger than second.
4/18/06 - Seems like it wouldn't be too hard to plot the trace norm for the unconstrained 2-D case. Two observations make our work easier: (1) the trace norm is invariant to rotation (so the orientation of the first vector can be arbitrary), and (2) the trace norm scales as the scale of the matrix, i.e. ||cX||_Σ = c||X||_Σ (so the magnitude of the first vector can be arbitrary). The X matrix is

1 0

x y

We use w to parameterize the basis matrix, V,

w √(1-w²)

√(1-w²) -w

Lengths in the basis directions are:

X₁ X₂ Length

V₁ w xw + y√(1-w²) √{w² + y² - y²w² + x²w² + 2xyw√(1-w²)}

V₂ √(1-w²) x√(1-w²) - yw √{1 - w² + x² - x²w² + y²w² - 2xyw√(1-w²)}

The maple code used to make the above calculations:
```
a := w;
b := x*w + y*sqrt(1-w^2);
expand(a^2+b^2);
a := sqrt(1-w^2);
b := x*sqrt(1-w^2)-y*w;
expand(a^2+b^2);
  
```
Here's how you calculate the trace norm of X (over x ∈ [-1,1], y ∈ [-1,1]):
```
n = 51;
x = ones(2*n-1,2*n-1,2*n-1);
y = ones(2*n-1,2*n-1,2*n-1);
w = ones(2*n-1,2*n-1,2*n-1);
z = ones(2*n-1,2*n-1,2*n-1);
for a=1:(2*n-1)
  a
  for b=1:(2*n-1)
    for c=1:(2*n-1)
      xx = (a-n)/(n-1);
      yy = (b-n)/(n-1);
      ww = (c-n)/(n-1);
      x(a,b,c) = xx;
      y(a,b,c) = yy;
      w(a,b,c) = ww;
      bl1 = sqrt(ww^2 + yy^2 + xx^2*ww^2 - yy^2*ww^2 + 2*xx*yy*ww*sqrt(1-ww^2));
      bl2 = sqrt(1 - ww^2 + xx^2 - xx^2*ww^2 + yy^2*ww^2 - 2*xx*yy*ww*sqrt(1-ww^2));
      z(a,b,c) = bl1 + bl2;
    end
  end
end
[zz,ww] = min(z,[],3);
mesh(x(:,:,1),y(:,:,1),zz);
xlabel('x');
ylabel('y');
zlabel('trace norm');
  
```
Here's the plot:

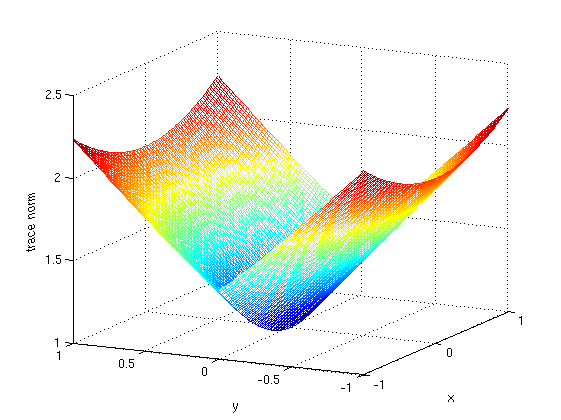
The trace norm plot where both vectors of X are unit length corresponds to values of the above plot as you trace a unit circle in the xy plane.

	X₁	X₂	Length
V₁	w	xw + y√(1-w²)	√{w² + y² - y²w² + x²w² + 2xyw√(1-w²)}
V₂	√(1-w²)	x√(1-w²) - yw	√{1 - w² + x² - x²w² + y²w² - 2xyw√(1-w²)}

4/17/06 - Okay, here's an attempt to make sense of one of these plots. Assume we have two unit-length vectors. Wlog, we can assume that one of them is (1,0). The other is (x,√(1-x²)). To calculate the trace norm, we must establish a basis. The first basis vector determines the basis: (y,√(1-y²)). The second basis vector is (√(1-y²),-y).

1st vector	(1,0)
2nd vector	(x,√(1-x²))
1st basis	(y,√(1-y²))
2nd basis	(√(1-y²),-y)

Lengths in the basis directions are:

	1st vector	2nd vector	Total Length
1st basis	y	xy + √[(1-x²)(1-y²)]	√{1 - x² + 2x²y² + 2xy√(1-x²)√(1-y²)}
2nd basis	√(1-y²)	x√(1-y²) - y√(1-x²)	√{1 + x² - 2x²y² - 2xy√(1-x²)√(1-y²)}

The maple code used to make the above calculations:

a := y;
b := x*y + sqrt((1-x^2)*(1-y^2));
expand(a^2+b^2);
a := sqrt(1-y^2);
b := x*sqrt(1-y^2)-y*sqrt(1-x^2);
expand(a^2+b^2);

Here's a plot of (what I call) the genearlized trace norm (sum of singular values, using basis vectors as the singular vectors---minimum over bases is the actual trace norm):

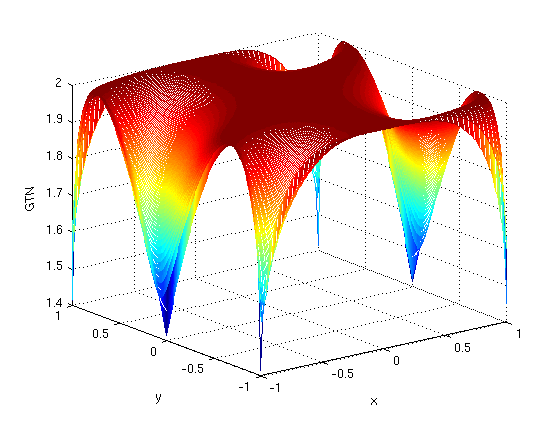
Note that the above plot is symmetrical about the origin. Bottom left is y-axis. Bottom right is x-axis. Left is z-axis. Here's the plot of x vs. trace norm (minimum over y-axis of above plot):

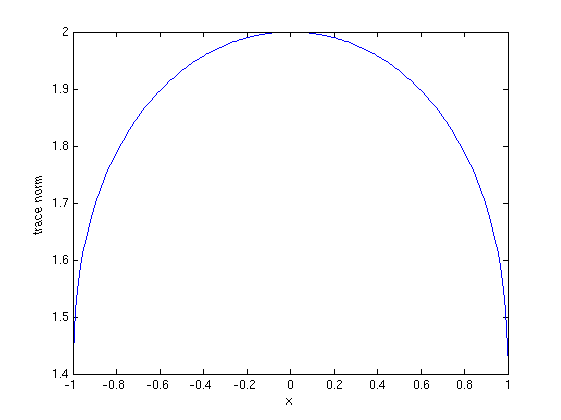
Note that this is identical to the plot of √x + √(2-x) for x ∈ [0,2]. Here's the matlab code used to generate the plots:

hold off;
n = 101;
x = ones(2*n-1,2*n-1);
y = ones(2*n-1,2*n-1);
z = ones(2*n-1,2*n-1);
for a=1:(2*n-1)
  for b=1:(2*n-1)
    xx = (a-n)/(n-1);
    yy = (b-n)/(n-1);
    x(a,b) = xx;
    y(a,b) = yy;
    bl1 = sqrt(1 - xx^2 + 2*xx^2*yy^2 + 2*xx*yy*sqrt(1-yy^2)*sqrt(1-xx^2));
    bl2 = sqrt(1 + xx^2 - 2*xx^2*yy^2 - 2*xx*yy*sqrt(1-yy^2)*sqrt(1-xx^2));
    z(a,b) = bl1 + bl2;
  end
end
mesh(x,y,z);
xlabel('x');
ylabel('y');
zlabel('GTN');
% trace norm calculation
[zz,yy] = min(z,[],2);
plot(x(:,1),zz);
xlabel('x');
ylabel('trace norm');
hold on;
x = 0:0.01:2;
plot(x-1,sqrt(x)+sqrt(2-x),'r');

4/16/06 - Each singular value is the length of a vector. The components of that vector are the dot-products of each data vector with the corresponding singular vector.
4/16/06 - What is our x-axis variable? Lengths in the different directions. Is that what the singular values are? Well, not exactly.
4/16/06 - Hmm... what about each of n vectors has fixed length, but their orientations are allowed to change? That's even more restrictive than constant Fro norm.
4/16/06 - Now, what's the scenario? Three vectors, and the frobenius norm of the stacked matrix is one. I.e. sum of squared entries of the vectors is one. Should it be Fro norm equals 1, or sum of lengths of vectors equals 1? Should be sum of vector lengths is constant.

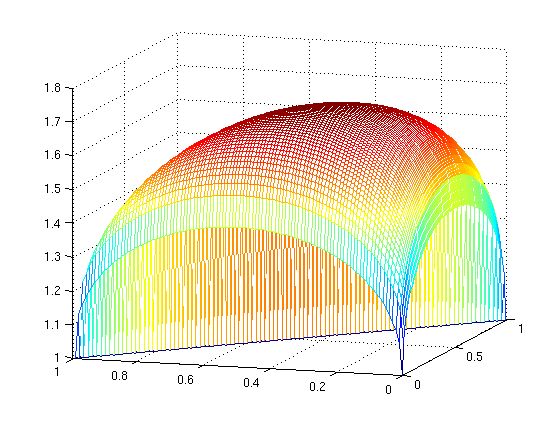
4/16/06 - What about a 3-D plot? Let x ∈ [0,1], y ∈ [0,1-x], f(x,y) = √x + √y + √(1-x-y). Here's what f(x,y) looks like:

Here's the matlab code to generate the plot:

  n = 101;
  x = ones(n,n);
  y = ones(n,n);
  z = ones(n,n);
  for a=1:n
    for b=1:n
      x(a,b) = (a-1)/n;
      y(a,b) = (b-1)/n;
      if a+b <= n
        z(a,b) = sqrt((a-1)/n)+sqrt((b-1)/n)+sqrt(1-(a-1)/n-(b-1)/n);
      else
        z(a,b) = 1;
      end
    end
  end
  mesh(x,y,z);

4/16/06 - Let x ∈ [0,1]. Let f(x) = √x + √(1-x). Here's what f(x) looks like:

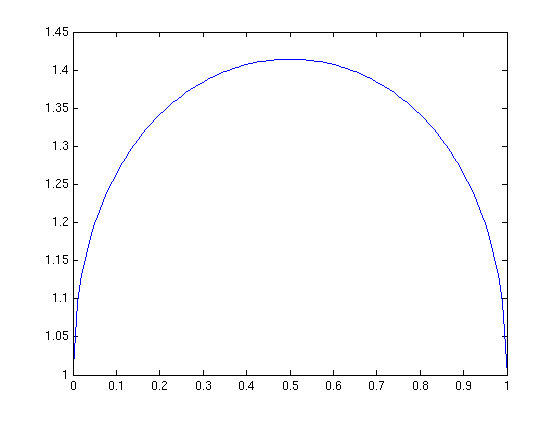
Here's the matlab code to generate the plot:
```
  x=0:0.01:1;
  plot(x,sqrt(x)+sqrt(1-x));
  
```
4/14/06 - Hrm... trace norm is actually similar to entropy and sine. Let c be the frobenius norm of the matrix. Plot the square root function from 0 to c. Draw a straight line from (0,0) to (c,√c). Rotate until this straight line is horizontal. Similar to entropy and sine, no? :) Here's how you generate it (c=10), with entropy & sine too, so that end points and max height align:
```
  hold off;
  x = 0:0.01:10;
  tnmax = max(sqrt(x)+sqrt(10-x)-sqrt(10));
  plot(x,(sqrt(x)+sqrt(10-x)-sqrt(10))./tnmax,'b'); % trace norm
  entmax = max(-x/10.*log(x/10)-(10-x)/10.*log((10-x)/10));
  hold on;
  plot(x,(-x/10.*log(x/10)-(10-x)/10.*log((10-x)/10))./entmax,'r'); % entropy
  x = (0:pi/100:pi)*10/pi;
  plot(x,sin(x*pi/10),'g');
  
```
Here's the plot itself:
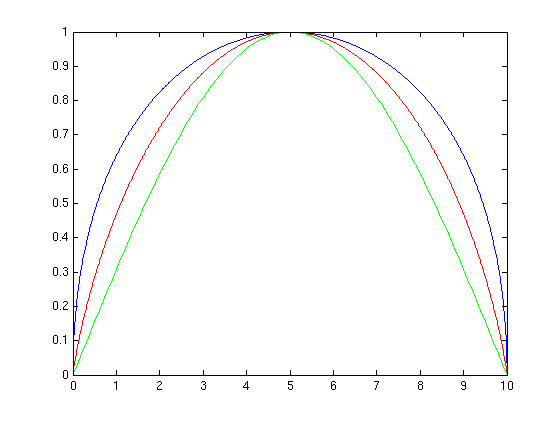
Trace norm is in blue, entropy is in red, sine is in green. All are scaled to unit max and (0,10) endpoints. A nice way of communicating this connection might be via the derivatives. Also, would be good to establish this alternate entropy as its own thing before making the connection to trace norm.
4/14/06 - Trace norm: quantity under the square root sign(s) remains constant. How it is broken up between square roots determines the value. And, the most "separated" case is where the value for each vector has its own square root (case where trace norm is sum of vector lengths). Each vector has a set of values to which it corresponds that sum to the square of the length of the vector. When vectors are orthogonal, the calculation is
Σ_i √||X_i||²
When the vectors are not orthogonal, values are moved around. We're still taking the square roots of values that sum to a constant, but we're taking roots of larger and smaller quantities. Due to concavity of the square root, we end up with a smaller value.
4/12/06 - Tommi agrees that we can't learn mean parameters by maximizing the likelihood subject to a constraint on the parameter matrix (e.g. trace norm equals 1).
4/12/06 - Okay, I had it wrong with respect to the area/volume calculation Tommi and I talked about. Assume that X is square and X^TX=XX^T (condition required for determinant identity). Then, the unnormalized trace norm prior is one over the absolute value of the product of exponentiated eigenvalues. The determinant identity, det(X)=prod(eig(X)) gives us e^-||X||_Σ = |det(e^-X)|. But, this still isn't an area/volume. Only reason it's a product is because of the exponentiation. Within the exponent, it's a sum of singular values/absolute values of eigenvalues. Still not sure if there's anything interesting here...
4/11/06 - Does the transform between X and Θ for the mean parameters preserve angles in some way? In 2-D, it preserves sinθ. But, it seems like this might not be the case in higher dimensions. Would be good to do a write-up giving some intuition for the trace norm.
4/10/06 - I'd like to be able to sit down with an experienced text researcher and explain to them why the trace norm makes sense in the context of text. How does it related to traditional similarity measures used in text research?
4/10/06 - Might be of value to look at angle measurements and see if we can relate the trace norm to any of them. For example, find the vectors such that the sum of sinθ between the chosen vector and all other vectors is minimized. Another: chose the optimal ordering to minimize the following sum: sine of angle between 1st and 2nd vector, plus sine of angle between 3rd vector and line through 1st and 2nd vectors, plus sine of angle between 4th vector and plane defined by 1st three vectors, etc.
4/10/06 - Chatted with Tommi. We're back to the natural parameterization. In fact, Tommi noted that there may be a connection to volume with the trace norm of the natural parameter matrix. He noted that for a square matrix e^-||X||_Σ = det(e^-X). Note that the determinant is closely related to volume as it is the product of the eigenvalues of the matrix. We might be able to relate e^-X to the mean parameters. Though, now that I've had a second chance to look at it, I'm not so sure. First, the sign is wrong (mean parameters are of the form e^x). Second, mean parameters exponentiate the individual values, not the eignenvalues (which is what happens with matrix exponentiation). Trace norm is more closely related to the sum of lengths of sides of the smallest bounding cube (though this still isn't a particularly good characterization).
4/7/06 - After having written about why using natural parameterization with the trace norm prior, I now am unsure of myself. I thought it was bad because documents with opposite topics would yield a relatively low trace norm. But, this is only the case if you assume a fixed "origin." If you allow the origin to be optimized, this phenomenon is not observed---two close document yield lower trace norm than two "opposite" documents of similar length.
4/5/06 - Some observations:
- The trace norm prior has a heavy tail since the negative exponent is length (much flatter than a Gaussian-type distribution). However, using it as a prior on a matrix of multinomial parameters (unit Euclidean length normalized per row), this aspect of the distribution is (nearly?) inneffectual since we are considering points that are approximately the same distance away from the origin. To take advantage of this flat-ness, with respect to how term frequencies are distributed, we would need to apply it more directly to the term frequency data (or maybe use a likelihood model that is similar to the multinomial, but includes expected document length in the parameter).
- It is appropriate to use one multinomial model per document, as the document is not clearly more finely divided. Multinomial can accurate model a single TF vector. It's only accurate for multiple TF vectors if they were really generated from multinomials (or some similarly heavy-tailed distribution).
- Integrating exp(-||X||_Σ) over matrices with unit row lengths is not going to be an easy task... After doing the change of variables to SVD, what are the limits of integration?!?!?
4/5/06 - Can we use a trace norm prior on the multinomial parameters? Only issue is: how do we constrain row lengths to 1? The trace norm of a matrix of multinomial mean parameters does give a good sense of the rank of the matrix. Though, there is the L1 vs. L2 issue. Would give a better sense of rank if each row were L2 normalized (rather than L1 normalized). What if we were to constrain to positive and L2 length 1, then renormalize to L1 length of 1 for the likelihood?
4/5/06 - The α parameters in LDA simply affect the per-document multinomial distribution over topics. They directly impact how often each topic is selected. This simply allows LDA to fit the data, it doesn't seem to provide any useful generalization power. LDA uses a Dirichlet prior on the topic indicators, not directly on the opics themselves. What if we were to place a prior directly on the topics? Say we place a trace norm prior on the multinomial parameters. Is this like placing a prior directly on the topics? I think so.
4/5/06 - It makes no sense to do trace norm clustering on natural parameters of the multinomial. Low-norm clustering of the natural parameters encourages topical opposites to be in the same cluster! Is there a trace norm based clustering that makes sense? The trace norm is a generalization of the gamma distribution (with k=1). And, normalized output from a gamma distribution are distributed like a Dirichlet. Only issue is that there are no parameters to control the trace norm distribution like there are to control the Gamma. Are the Gamma parameters necessary and/or useful? They serve as topic priors/weights in LDA.
4/4/06 - Ah ha! Low-norm natural parameter clustering is terrible for text because it encourages topically opposite documents to be placed in the same cluster. In natural parameterization, a document's opposite is simply its negation. Hence, an algorithm with the goal of creating low-rank clusters would combine opposites. Not good! Might actually make more sense to use the mean parameterization!
4/4/06 - There are three basic types of clustering algorithms: (1) center-based (e.g. k-means), (2) spectral (e.g. Ng/Jordan/Weiss NIPS paper), (3) low-rank (trace norm clustering). Question we need to answer: is low-rank clustering the appropriate thing for text? Is small angle between data points more important than small distance?
4/4/06 - One thing MMMF provides us with is a set of topics/themes. These are the rows of ΣV^T. U specifies the composition of each item in terms of "topics." Rows of U are points on the sphere. We could do a k-means type clustering on the rows of U to arrange points into "flat" clusters. Think of trace norm clustering as being a generalization of center-based clustering algorithms? Center-based clustering is a subroutine of trace norm clustering.
4/4/06 - Doesn't the SVD provide us with the optimal rotation matrix? Optimal rotation would put top k₁ singular values in 1st cluster, second k₂ s.v.'s in 2nd cluster, etc. Hmm... this does not sound like a very good way to cluster...
4/4/06 - How do I determine the best allocation of data into fixed size clusters? Say you have a 3 × d matrix and you take the trace norm of the first two rows plus the trace norm (Euclidean norm) of the last row. What if you allow a rotation of the matrix? The rotation won't change the trace norm of the full matrix, but it will affect the sum of individual trace norms. One idea for fast, approximate learning of allocation of data into fixed slzed clusters is to a rotation matrix that yields the smallest sum of trace norms. Then, "clip" values so that there is one "1" in every column/row.
4/4/06 - In order to do bottom-up clustering properly, we need to find the "critical points"---the values of λ for which multiple clusterings are equally good. The simplest explanation of how to do bottom-up clustering is to calculate the score for each clustering as a function of λ, then increase λ from zero toward ∞, noting the clustering with maximum probability at each value of λ.
4/3/06 - I need to modularize the clustering code. I have a function to calculate the negative log-likelihood ("score"). But, it's not general. m3fScore needs to accept a number of parameters:
- Data
- Log normalization constant values
- Objective/derivative function
- Size of parameter space
- Lambda
4/3/06 - Before I embark on the hierarchical model, I think I should do the simple, obvious thing of comparing smoothed log-odds frequency rates of words for each cluster. This will give us a quick-and-dirty way of inspecting each cluster. I should also implement bottom-up clustering.
4/3/06 - This "alternate parameterization" I'm thinking of doing for the natural parameter multinomial is really just the hierarchical model Tommi and I talked about last Sept./Oct.
3/31/06 - For 95% confidence interval, why can't we just find the middle 95% range of values? Why would we want to do a Normal approximation?
3/31/06 - In his Weighted Low Rank Approximation paper, Nati discusses (in section 3) the idea of low-rank Logistic Regression (and related techniques). He also has discussion (in section 2.1) of the optimization surface of matrix factorization problems---closely related to the optimization problems we're considering.
3/31/06 - Subtracting mean is exactly like subtracting magnitude of (1,1,1,...,1) vector. Since we are only subtracting the actual magnitude compoonent, we always decrease the length. Similarly, for SVD, we decrease the magnitude of each singular value by the corresponding magnitude in the (1,1,1,...,1) direction. Might need to adjust the basis to get the correct singular values, but readjusting like this always decreases trace norm. So, yes, subtracting mean decreases the trace norm.
3/31/06 - Will subtracting the mean from all rows of a matrix always decrease its trace norm? This is certainly true for a vector, since trace norm is just length :) Though, how do we show that subtracting mean is certain to reduce length? Subtracting vector mean is like separating the vector into two components, (1) parallel, and (2) perpendicular, to the (1,1,1,...,1) vector. The perpendicular is certainly shorter than then entire vector (since it has no parallel component).
3/31/06 - Seems that it would be good to "center" the natural parameter values. Currently, they're affected by the frequency with which the word occurs. A common word will have all positive values; a rare word might have all negative vales. Note that a zero value corresponds to frequency equal to 1/V, where V is size of vocabulary.
3/27/06 - Read the first three chapters of Thomas Minka's thesis on Expectation Propagation. I don't think EP will be useful for estimating the trace norm distribution partition function, at least if we were to use a Gaussian as the approximate distribution. Trouble is that the Gaussian approximation can't deal well with a distribution with multiple modes. Minka includes a specific example of this, showing poor performance from EP (along with most methods). Importance sampling is the top-performing methods (which is what we are currently using). Possibly worth noting is the fact that the variational approach he uses performs poorly.
3/27/06 - ICA assumes that there are n independent components that are linearly mixed. ICA tries to identify those independent components. One might view trace norm clustering as a generalization of (PCA-style) ICA. Trace norm clustering assumes that there the components are grouped such that each group is independent of the others, but that components within each group are highly dependent. Learning of the linear transform can be thought of as the clustering operation (esp. if the linear transform matrix is required to have orthonormal or probabilistic columns/rows).
3/26/06 - ICA is related to trace norm clustering, but the tie is somewhat loose. In ICA, the goal is to find a linear transform, W, of a random vector, x, so that components of the output, s=Ax, are "independent". ICA is not a fixed, standard algorithm because people have devised many different ways of estimating independence. In practice, x is not a variable, but rather samples from a variable. I.e. in reality, we're given a matrix X and we want to find a linear transform W so that the rows of S=WX are "independent." Note that PCA is an ICA method where the notion of independence is orthogonality (or uncorrelated, after having subtracted the mean from each row).
3/24/06 - Chatted with Alan. He said this looks a lot like ICA. We need to look at ICA and compare. What's similar, what's different. Alan noted that ICA can deal with the case of not completely orthogonal components. He also suggested that we look at using expectation propagation for solving the partition function. He says that it handles each difference term one-at-a-time, incorporating each into a single n^th order polynomial-type term.
3/24/06 - Tommi suggests that it might be valuable to provide a negative result for clustering, along with a good explanation of why (with the corresponding intuitions). I.e. go ahead with the clustering experiments on the chowhound data. Try it at various levels of granularity---sentence, post, thread---and report on how well it works. Also, compare vs. other dimensionality reduction/clustering methods.
3/23/06 - Remember that for chowhound data, we are treating each thread as a post---might even be worth looking at segmentation at the post level (is the reply on the same topic?).
3/23/06 - Problem with the topic segmentation task is that a quick look at the data tells me that it's not useful/interesting. There is relatively little topic-switching within a message and I think it would be difficult to identify using only term frequency statistics. NLP cues look much more important for finding topic changes
3/23/06 - Goals for today: (1) prepare chowhound data for topic segmentatoin task, (2) read group meeting paper.
3/22/06 - Okay, my original reasoning was correct. The inequality over normalization constants does hold. Note that we are integrating over ℜ^{10 × 10}. No issue breaking up the integral b/c all limits of integration are all [0,∞). As long as log Z is always non-negative, then the larger matrix always has the larger normalization constant.
3/22/06 - Ah ha! But, we can prove my "gut" correct using the basic trace norm inequality. Let X ∈ ℜ^{10 ×
10} and let X₁ and X₂ be a partitioning of X so that X = [X₁; X₂]. Then, ||X||_Σ ≤ ||X₁||_Σ + ||X₂||_Σ and log Z(X) ≥ log Z(X₁) + log Z(X₂). The last inequality is true b/c the integrals are over the same volumes. ACK! No they're not! The limits of integration differ! Argh!
3/22/06 - Something I've been taking for granted may not be true. While it is true that the trace norm of a matrix is always less than the sum of trace norms of any partitioning, and that the reverse relation holds for the corresponding log-normalization constants, it is not true that there is a clear relationship between normalization constants for different size matrices. Consider Z_{10 ×
10} and Z_{10 × 9}. My gut says that Z_{10
× 10} ≥ Z_{10 × 9}. But, (1) a 10 × 10 matrix which is a row update of a 10 × 9 matrix will always have a larger trace norm (than the 10 × 9 matrix), and (2) the integrals are over different volumes, so they aren't directly comparable.
3/22/06 - I need to re-focus on the application/task-at-hand. Recall topic segmentation by sentence. How do we make this work? One thing we could try would be to perform clustering on the rows produced by MMMF (NLL is loss function). I'm kinda bummed about the trace norm clustering stuff---that damn normalization constant is too hard to calculate! I suspect that the method of sampling to estimate doesn't work very well. And the variational approximation isn't implemented yet...
3/20/06 - While working on the paper, John & I more-or-less determined that the normalization constant is too difficult to calculate in order for its use to be practical. We also determined that it may be relatively easy to put bounds on the norm. const. for different size partitionings. Let X ∈ ℜ^{k × n} where n is fixed. Let
Z_k = ∫ exp(-||X||) dX
be the normalizing constant of the trace norm distribution for X. Adding a non-zero row to a matrix increases its trace norm, so clearly Z_k < Z_k+1. We have examined log-normalization constants for straddled clusters. Let k > 1. We have observed that
log Z_k + log Z_l < log Z_k-1 + log Z_l+1
I.e. there is a natural order over partitioning sizes that is determined by the normalization constant. We are intent on proving this inequality generally. This would greatly reduce our need to calculate the normalization constant, as we could eliminate many partioning sizes as impossible due to a more fine and more coarse clustering having better objective via this inequality.
3/20/06 - We submitted a paper to UAI! Woo hoo!

Jason Rennie
Last modified: Thu Sep 14 14:53:17 EDT 2006